|
||||
| Robots should have eyes, see the environment, and perform their actions guided by vision. Of cause this has been a topic of artificial intelligence and as early as in the 1960's AI researchers like Marvin Minsky and Seymour Papert (the father of Lego Mindstorm) hooked together computers, TV cameras, and robotic actuators to build towers from individual blocks and to navigate through buildings. Nowadays some industrial robots have vision. Here is a homebrew version: |
||||
 |
My experimental setup consists of a webcam
(QuickCam VC), a set of mirrors to generate a stereoscopic (3D) view, and a robotic arm
with a hand. The robotic arm can move left/ right, (x-direction), up/ down
(y-direction), and back/ forth (z-direction). The hand can close and open - all
these movements are generated by 4 servos (Futaba FP-S28). The hand is from a Lady-Robot and it has two red-colored fingernails. |
|||
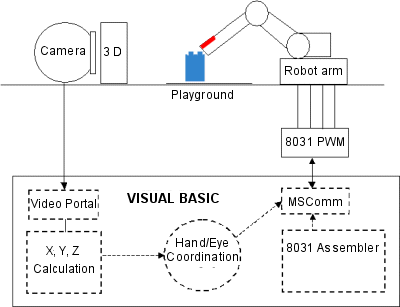 |
The software is written in Visual Basic VB5. The camera comes with a Visual Portal Module to interface the camera to Visual Basic programs. I wrote a program that calculates the coordinates x, y, z of the objects in the playground from the picture. Then my program calculates the necessary movements of the arm and sends the data via a serial port to the servos. An 8031 Microcontroller converts the signals to Pulse Width Modulation (PWM). An 8031 Assembler (written by my son Hanno) allows the modification of the servo routines. |
|||
First, the robot should know where objects are - if possible in 3 dimensions:
3D Vision
A simple example of 3D vision is shown in
the following picture:
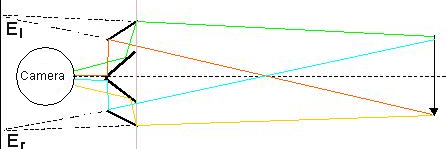 |
For stereoscopic vision I use one camera with 4 mirrors. The lightpath is shown above. The mirrors generate virtual eyes, El and Er, which look at the scene from a left and a right viewpoint.
 |
The left and the right view are slightly different (disparity). The next picture shows the light intensity along the scan line along the left and the right part of the image. The program finds the corresponding edges from the objects and calculates the distance of the objects from the disparity. The result is shown in the third picture - a bird's view: there is a big object in the back and a small object in the front.
Colors
|
|
The first picture shows several test colors. According to
Young's Theory colors are the sum of RED, GREEN, and BLUE components, e.g. yellow is the
sum of red and green. A scan across the test colors shows the RGB
signals of the camera. Yellow has strong red and green signals and only a weak blue
component. For further signal processing it is helpful to calculate color
opponents; the ratios red/green and blue/yellow are shown in the color map.
The different regions for blue, green, yellow, white, and red are clearly separated and
can be evaluated by a computer program. |
||
|
|
Object Recognition
Object recognition for simple objects is
shown in the following pictures.
|
||
| First several objects are shown to the camera; the program frames the object, resizes it to a standard size, and adds the picture to the gallery. In the recognition phase the test picture is compared to pictures in the gallery. Comparison is done by correlation, where corresponding picture values are multiplied and summed. |
||



